Ejaad-Nama 0x13: What knot to do...
Ejaad-Nama (Urdu: Letters of Invention). We talk about lemons, acid batteries, and anything in between.
Ejaad-Nama is the word from the Urdu language which means Letters of Invention. Ejaad-nama is about improving scientific literacy and normalizing it. By removing the barriers to learning science, we aim to create a community that contributes to society more than just in one meaningful way. You can subscribe here to get the regular update in your inbox:
Let us get Knotty! ;)
I am one of those people who hates tying my shoelaces. That’s because, no matter what I do, they always get untangled. That’s contrary to my experience of owning a wired headset or earbuds. No matter how neatly you tie/coil them, or keep them on your desk, they magically find a way to be tangled. It’s a problem everyone has tried to solve by watching one of those 5-minute craft videos which never seem to work in real life. I know you have tried to keep the wires from tangling. But why? If they are gonna keep tangling.
I think more important question is why knot? Lets try to untangle some knots. Last of the bad puns. I promise.
Recently, I stumbled upon a research paper titled “Spontaneous knotting of an agitated string” which investigates the science behind the black magic of knot forming in a piece of string. Since I enjoyed going through the research paper, I realized I could make the scientific paper a simpler read for everyone to enjoy.
The Basics
Knot theory is an area of mathematics and topologies which studies the properties of mathematical knots. In topology, shapes are considered the same if they can be deformed or changed without cutting them e.g. a circle and a square are essentially a circle as they both are closed. You can make a square from a rubberband. Or stretch it to have a triangle. Its the same shape just shape shifting like Prof. Mcgonagall.
A mathematical knot differs from the real-life one in that the ends are always joined together. Like cutting the rubberband, tying up a knot and stitching back the ends again.
For example, the trefoil knot below is the most non-trivial knot which cannot be undone. Hence, a knot is defined as a continuous closed loop that cannot be untangled into a simple loop.
Knot Classification
Knots are classified according to the number of times it crosses under/over itself. To further tabulate and document them, Knot projections are created which serve as 2D projection of the knot. This is equivalent to looking at a shadow of the knot when light is shining on it. Below are some of the prime knots. The first number represents the number of crossings, while the subscript represents the index of the knot which have the same number of crossings. e.g. 2 knots have 5 crossings: 5(1) and 5(2).
However, in classifying the knots, the rules of topology apply: Two knots are considered to be equivalent if they can be deformed into each other without cutting them. If you take a rubberband, fold it and tie a knot, its still not considered a knot as you can untie it to its original shape.
Take for example the unfolding of the following knot which is actually an unknot.
Knot theory often revolves around the fundamental question of how to tell the knots apart from each other. Since last 100 years, plenty of knots have been tabulated and recorded.
This is done by creating polynomial expressions about a knot and manipulating them. Knot theory is used in understanding how DNA structures can be untangled.
Another interesting use has been in cryptography: encryption and decryption. If you look at the gif above, it requires specific steps to untangle a knot into unknot. By mathemazing the knots, these properties is used in secure messaging.
But…….how do I untangle my wiring mess?
Now that you understand how complicated knots can get, Researchers at the University of Chicago investigated the formation of knots. They wanted to know why do their ear buds get so tangled up in their bag riding a public train to office.
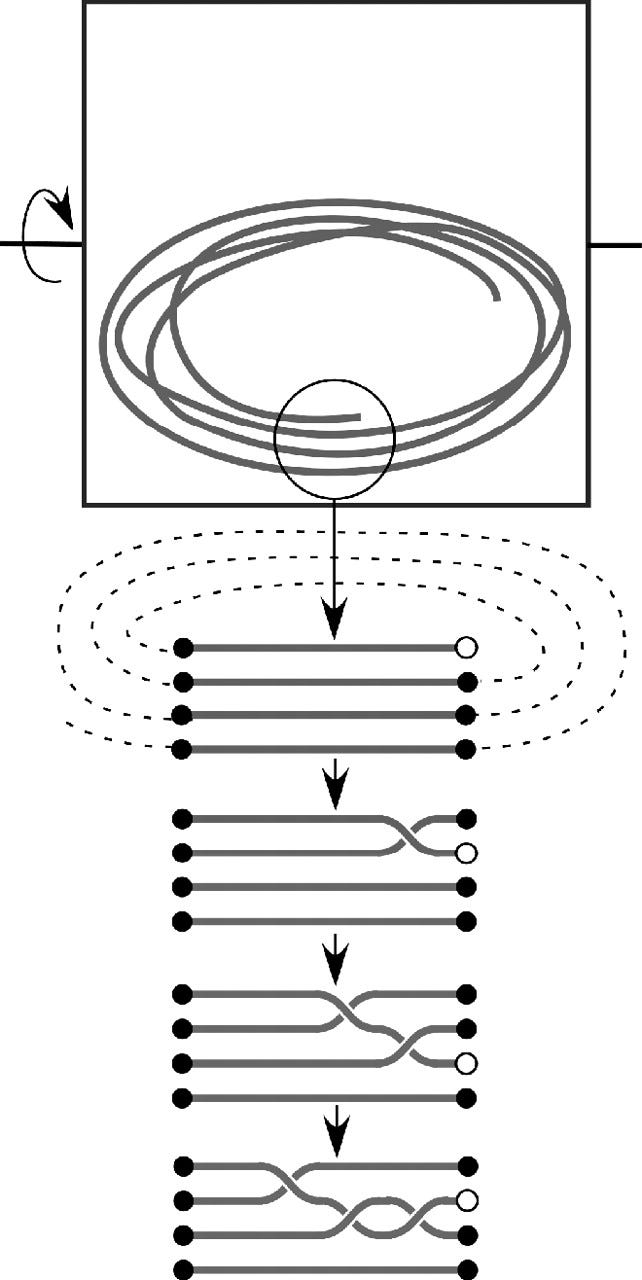
They investigated by throwing a coiled up string(your earphones) in a spinning box(your backpack). They took the images of the tangled knots and compared them with the classified and tabulated unique knots.
The paper provides a theory on how the knots are formed. Basically, the coiled-up open end of the string ends parallel and resting on the wire. As the box moves, the open end falls over the wires ending up in a braid formation.
Interestingly, the likelihood of knotting your wires depends on several factors:
Length of the wire
It seems that below 46 centimeters, the probability of knotting your wires is close to impossible. However, most common earbuds such as Apple earbuds are 139 cm which puts them right at coin toss likelihood of getting tangles. Interestingly, after a certain string length, the probability of getting tangled does not increase. This is because, the longer the wire gets, the more chances it gets to untangle itself while tangling itself.
Beyond 1.5m, the probability of the entanglement saturates. Interestingly, the mean number of crossings and types of knots also saturate exactly in the same manner. Most of the knots are of type 3 (trefoil knot). That could explain why we get good over time in untangling our wires: we just get so much practice with the same knots.
Confined space
The data also shows a correlation between the space the string is stored and how probably it is to knotting. The tighter the space, the less the probability of getting your wires tangled. That’s also the reason umbilical cord knots in baby births are rare as well. The womb is a very confined as a cozy place to be in.
Flexibility of the cable
The more flexible the cable is, the more freely it will move to achieve the braided configuration. The stiffer the cable is, the more it will try to stay in shape and not move about. This is also true for flat cables that are often advertised as tangle-free. This is because the flatter cables cannot move easily in the narrower directions.
Hence, If you were to have a small earpiece cord that is flat and stiff, rolled up in a tight box or a tiny pocket, you may have your life tangle-free.
(I might make this a regular thing of writing research papers in an easy and fun way. If you liked it, Do throw me some feedback in the comments.)
If you would like to send in your projects and hacks to be part of the newsletter, please do comment below, or email me: a.nadeem89@gmail.com. Leave your feedback in the comments about the content. and subscribe here, and share the newsletter with your friend.














yes i like this idea of simplifying research papers especially for common questions. some topics id like to know about:why lassi or certain milk products make us sleepy
colour theory
chaos theory etc
Keep it up!
Knots are interesting! Thank you for writing this!